1.Scrieti ecuatiile parametrice pt curba:

2.determinati lungime curbei:

multumesc

[Citat] 1.Scrieti ecuatiile parametrice pt curba:

Ceva nu este in regula cu ecuatia de mai sus.

[Citat] 2.determinati lungime curbei: multumesc

Curba este inchisa. Folosim parametrizarea

Atunci

Lungimea curbei este

da asa e
am gresit eu

ec e:

[Citat] da asa e am gresit eu ec e:

Imi arunc privirea asupra problemei de mai sus, si constat ca sunt deprimat. De ce am avea nevoie de o parametrizare? Teorema functiilor implicite ne garanteaza existenta locala a acestei curbe.

Poti sa revii cu cerintele complete si clare? Se vrea o reprezentare parametrica explicita (sub forma de 'formule') ??? se vrea o reprezentare parametrica locala, in jurul unui punct? Ca fapt divers, ecuatia de mai sus este reuniunea a doua curbe ce se intersecteaza in origine.

noua ni s'a dat un pdf(defapt erau mai multe) cu probleme care vor aparea pe biletele de examen!
Una din ele era chiar asa cum am propus-o aici:Sa se scrie ecuatiile parametrice pt curbele...si apoi o lista frumoasa de curbe cica.
Ma gandesc k o fi vrand sa vada o aplicare a teorie(pe care nu o am) pe exemplu concret..sa se gaseasca un x=.... si y=.....

spre ex: pt curba

si ec parametrice:

[Citat] ec e:

OK. Si noi am gresit partial cand am spus ca este o reuniune de doua curbe.
In orice punct diferit de origine, ambele coordonate sunt nenule. Notam

Obtinem ecuatia

Tinand seama ca y este nenul, putem simplifica

si obtinem

Inlocuind in prima relatie si avem

Iata si cum arata curba cu pricina:

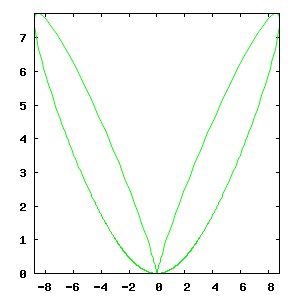
Evident, nu orice curba definita implicit poate fi parametrizata in acest mod. De asemenea, problema este interesanta doar din punct de vedere algebric.

multumesc.

1.Fie curba

. Sa se arate ca tangentele in 3 puncte coliniare retaie curba in 3 puncte coliniare.

2.Sa se afle infasuratoarea si locul geometric al punctelor singulare pt familiile de curbe
a)

daca

3.Fie curba

si suprafata

.Sa se arate ca C inclus in S si planul oscilator la curba coincide cu planul tangent la suprafata.

4.Fie curba

.Sa se arate ca:
~curba se fala pe un con si taie generatoarele conului sub un unghi constant
~tangentele la curba fac un unghi constant cu axa Oz

atat.

[Citat] multumesc. 1.Fie curba . Sa se arate ca tangentele in 3 puncte coliniare retaie curba in 3 puncte coliniare.

Trebuie spus in ipoteza ca a este nenul.

Solutia naiva. Pasi de urmat:

• Parametrizam curba:
  
  
  
  
• Calculam vectorul tangent
  
  
  
  Ecuatia tangentei, scrisa in mod parametric este
  
  
  
  
• Intersectam aceasta tangenta cu curba si gasim (in cazul in care t este nenul) ca punctul de intersectie are coordonatele
  
  
  
  
• Reformulam ipoteza: Numerele
  
  satisfac identitatea
  
  
  
  Valoarea determinantului poate fi calculata explicit, iar ecuatia de mai sus se rescrie
  
  
  
  
• Avem de arata ca ecuatia precedenta implica si:
  
  
  
  sau, dupa simplificari:
  
  
  
  ceea ce este, evident, adevarat.
  

Indicatie pentru solutia 'pro'. Curba este o curba cubica. Orice dreapta din plan o intersecteaza in cel mult trei puncte. Dupa cum se vede, directia inspre care o ia cursul pe care-l urmezi este (posibil) spre curbe algebrice.

Curba are un punct singular, anume originea. Multimea

a punctelor de pe curba poate fi organizata intr-o structura de grup comutativ in felul urmator:

Oricare trei puncte colineare

verifica

in acest grup. Nu suntem 100% siguri de acest fapt, valabil indeobste pentru asa-zisele curbe eliptice; verifica cu teoria de la curs. Regula de mai sus este valabila si pentru cazul in care doua din puncte coincis, caz in care se foloseste tangenta in acest punct.

Folosind structura grupului, sa nu uitam cum construim intersectia tangentei intr-un punct A cu curba. Pai, punctul C cautat trebuie sa satisfaca ecuatia

Revenim la problema. Ipoteza spune ca avem trei puncte

colineara, adica

Tangentele in aceste puncte taie din nou curba in punctele

Deoarece

rezulta ca si aceste trei puncte sunt colineare

[Citat] 2.Sa se afle infasuratoarea si locul geometric al punctelor singulare pt familiile de curbe a) daca

Nu intelegem problema. In mod normal familia de curbe trebuie sa depinde de un singur parametru. Verifica enuntul.

[Citat] 3.Fie curba si suprafata .Sa se arate ca C inclus in S si planul oscilator la curba coincide cu planul tangent la suprafata.

Formula de parametrizare nu este completa. Lipseste (probabil)

. In acest caz este simplu de verificat ca

Planul osculator este perpendicular pe vectorul binormal, care este la randu-i paralel cu

unde

Un mic calcul arata ca

Pe de alta parte, vectorul normal la suprafata intr-un punct (x,y,z) este paralel cu

unde

Mai precis,

Atunci cand

gasim ca cei doi vectori sunt paraleli, q.e.d.

Ca observatie, planul se numeste OSCULATOR, nu OSCILATOR.

[Citat] 4.Fie curba .Sa se arate ca: ~curba se fala pe un con si taie generatoarele conului sub un unghi constant ~tangentele la curba fac un unghi constant cu axa Oz

Ar trebui sa nu ai probleme. Sunt numai niste calcule plictisitoare. Revino daca te impotmolesti...

multumesc!!! rezolvat!!!
am luat 8!!!!!! \:D/ si asta din cauza k teoria ma omoara inclusiv demonstratiile lor interminabile!!
o sa revin intr'o sapt pt analiza:D

Curba data, de ecuatie

, este o curba singulara. Ea poate fi considerata a fi o degenerare a unei familii de curbe eliptice, de exemplu

.

Pentru curbe eliptice este cunoscuta inca de pe vremea lui

o teorema cu valoare estetica in matematica, care spune cam asa ceva:

Consideram multimea punctelor x,y,z ce satisfac o ecuatie de gradul 3 homogena, nesingulara, nedegenerata, cu proprietati "bune" (al carei gen este unu).
Sa zicem ca dreptele d1 si d2 taie curba in punctele A1, B1, C1 si respectiv A2, B2, C2. (Unele puncte pot coincide, multiplicitatile trebuie considerate corespunzator, nu am sansa sa definesc aici acet lucru de semiprofund inteles algebric.) Formam dreptele (unic determinate proiectiv, multiplicitatile joaca din nou un rol...)

prin A1, A2, care potrivit teoremei lui Bezout mai taie cubica in un al treilea punct A3,

prin B1, B2, care potrivit teoremei lui Bezout mai taie cubica in un al treilea punct B3,

prin C1, C2, care potrivit teoremei lui Bezout mai taie cubica in un al treilea punct C3.

Ei bine, atunci A3, B3, C3 sunt coliniare. (Ele se afla pe o dreapta d3, sa zicem). Un desen ar fi...

Aceasta teorema se poate demonstra estetic folosind structura de grup de pe curba eliptica. Exista carti specializate, relativ usor citibile pentru un elev interesat, intre timp gasibile electronic liber pe net. Eu il recomand pe Milne, Elliptic Curves, aici. Exista si alte demonstratii, dar mai sus a fost data o demonstratie bazata pe aceasta structura.

Pentru a face demonstratia data in cazul curbei degenerate considerate a fi VERITABILA, trebuie

fie specificata legea + pe curba degenerata si studiata mai indeaproape (degenerarea poate fi aditiva sau multiplicativa, in demonstratia naiva de mai sus imi lipseste de exemplu o referinta la faptul ca punctul singular este elementul neutru, hm, de ce avem de exemplu 0+0=0... si cum e + definit algebric folosind parametrizarea rationala standard, obtinuta taind curba data printr-o tangenta cu panta t, y=tx, prin punctul singular 0 = (0,0))

fie etablata o familie eliptica ce degenereaza la curba data, preluand teorema lui Weierstrass pentru fiecare membru al familiei si vazand ca degenerarea pastreaza coliniaritatea ceruta.

Aceste precizari le fac la cererea explicita a unei opinii neutre asupra solutiei prezentate, sub nici o forma drept critica, pentru a face clar ca limitele materiei de manual exista, dar si a faptului ca "matematica dura" este la un pas departare de materia de liceu, relativ accesibila. (Pe ecurbele eliptice este pus conjectura lui Birch si Swinnerton-Dyer, pe care sunt puse cateva lovele bune, suma ce se va multiplica pentru cel ce o demonstreaza cu 100, daca se va decide sa faca reclama la o bautura racoritoare sau alta...) Luati comentariul acesta ca o invitatie la a-l citi pe Milne, a instala pachetul PARI si a face "adunari" de puncte pe curbe eliptice, astfel intelegand si un secret cunoscut al criptografiei actuale. (Curbele eliptice se pot scrie nu numai peste corpul numerelor complexe, peste care am lucrat tacit ca sa tot am 3 puncte de intersectie, ci si peste un corp cu 2 la puterea 127 elemente. Pentru informaticieni, un punct bun de sapat estetic..) Hai ca ma gat aci...