[Citat]
Fiind date numerele complexe
astfel incat
. Sa se determine numarul real x astfel incat
.
|
Discutam mai intai conditiile de existenta.
Substituind
, avem
. Inegalitatea triunghiului,
, conduce la
. Aceasta inecuatie se poate scrie sub forma
. Functia din membrul drept este strict descrescatoare ca functie de 1/x si egala cu 1 pentru 1/x=2. Rezulta
.
Folosind identitatea
valabila pentru orice numere complexe, inecuatia de rezolvat devine
sau echivalent,
Pentru valori valori negative ale lui x, avem f(x)<0 caci
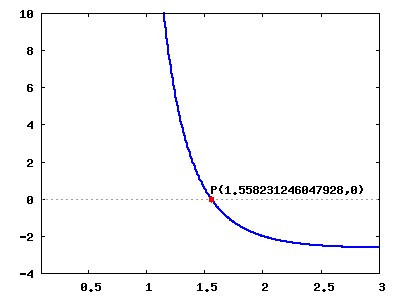
. Pentru valori pozitive ale lui x, studiind graficul lui f se observa ca
(nu se poate exprima printr-o formula exacta acest numar). In concluzie,