Aceasta este una din problemele pe care Paul Halmos le-a considerat ca merita incluse in cartea sa. Ideea este urmatoarea: sa presupunem ca taietura incepe si se termina pe doua laturi adiacente unui varf anume. Construim, pe rand, prin simetrie fata de laturi (in oglinda) copii ale triunghiului original.

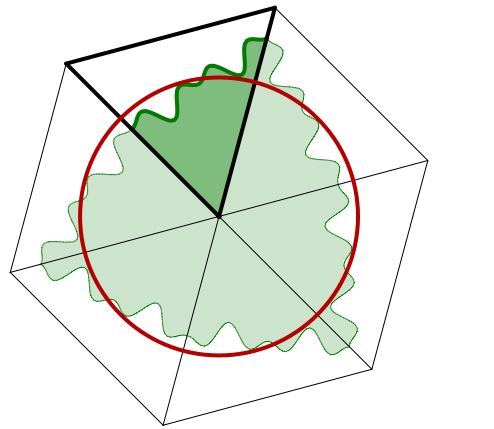
Atunci:

• Regiunea verde are perimetrul exact de sase ori lungimea taieturii
  
• Regiunea verde are aria exact jumatate din aria hexagonului, adica
  
  
  
  
• Perimetrul regiunii verzi este minim atunci cand frontiera sa este un cerc. In acest caz, notand cu
  
  raza cercului, trebuie sa avem
  
  
  
  

Lungimea taieturii minime este perimetrul cercului cu raza de mai sus, impartit la sase: