Rog sa ma ajutati!
1.Sa se afle valorile parametrului real m, stiind ca dreapta de ecuatie y=2x+1 este tangenta la graficul functiei f;D->R, f(x)=sqrt(4x*x+m)+3x.
2. Sa se rezolve in R ecuatia
log in baza (a*a-x*x)a lui (a*a*x*x-1)=1, unde a este parametru real.
3.Sa se determine raportul dintre volumele cilindrului si conului inscrise in aceiasi sfera, daca inaltimea cilindrului si cea a conului sint egale cu raza sferei.

[Citat] 1.Sa se afle valorile parametrului real m, stiind ca dreapta de ecuatie y=2x+1 este tangenta la graficul functiei f;D->R, f(x)=sqrt(4x*x+m)+3x.

Derivata in punctul de tangenta trebuie sa fie egala cu panta dreptei, adica 2. Din ecuatia

obtinem imediat

, de unde rezulta x negativ, apoi

, deci

. In acel punct trebuie sa avem si

. Deoarece

rezulta

Am obtinut x=-1/3 si

. Ne putem convinge de acest fapt si folosind figura dinamica de mai jos (slider-ul schimba valoarea parametrului m).

Figura

[Citat] 2. Sa se rezolve in R ecuatia log in baza (a*a-x*x)a lui (a*a*x*x-1)=1, unde a este parametru real.

Nu sunt sigur ca inteleg formula. Ecuatia este, cumva:

[Citat] 3.Sa se determine raportul dintre volumele cilindrului si conului inscrise in aceiasi sfera, daca inaltimea cilindrului si cea a conului sint egale cu raza sferei.

Daca r este raza sferei, atunci razele bazelor cilindrului si a conului sunt

respectiv

. De aici, raportul se calculeaza de la sine.

Buna seara!
Sunteti deosebiti! Multumim.

Ecuatia se prezinta exact asa. Mersi anticipat!

Ionela

[Citat] 2. Sa se rezolve in R ecuatia log in baza (a*a-x*x)a lui (a*a*x*x-1)=1, unde a este parametru real.

Conditiile de existenta sunt

. Ecuatia este echivalenta cu

, de unde

. Mai ramane sa discutam conditiile de existenta. Substituind valorile gasite ale lui x in conditiile de existenta, avem

Concluzia:

- daca

, atunci

-pentru celelalte valori ale lui a nu exista solutii

Cum oformam scrierea problemei>
Sa se determine toate valorile parametrului real a pentru care axa absciselor este tangenta la graficul functiei f:R->R, f(x)=a+9x-(x^3)/3?

Mc anticipat.

[Citat] Cum oformam scrierea problemei> Sa se determine toate valorile parametrului real a pentru care axa absciselor este tangenta la graficul functiei f:R->R, f(x)=a+9x-(x^3)/3? Mc anticipat.

Fie x abscisa punctului de tangenta. Conditia din enunt este echivalenta cu

• Punctul (x,0) apartine graficului functiei
  
• Tangenta in x este orizontala
  

Cu alte cuvinte,

, adica

De aici obtinem imediat

si in final

1.Fie ca este reprezentat graficul functiei f:R->R, f(x)=27-x*x si un triunghi isoscel MON, MN||Ox,MO=ON, punctele M si N, apartin parabolei si sunt situate in semiplanul de sus. Sa se determine aria maxima pe care o poate avea un astfel de triunghi.
2.Sa se determine valorile parametrilor reali a si b pentru care multimea solutiilor inecuatiei x^4+x^3-x^2+ax+b=<0 este intervalul [-2,1].

[Citat] 1.Fie ca este reprezentat graficul functiei f:R->R, f(x)=27-x*x si un triunghi isoscel MON, MN||Ox,MO=ON, punctele M si N, apartin parabolei si sunt situate in semiplanul de sus. Sa se determine aria maxima pe care o poate avea un astfel de triunghi.

Figura

Punctele M si N au coordonatele

. Aria triunghiului MON se exprima ca functie de x sub forma

Derivata functiei este

. Prin urmare, pe intervalul

functia S isi atinge maximumul in punctul x=3. valoarea acestui maxim este

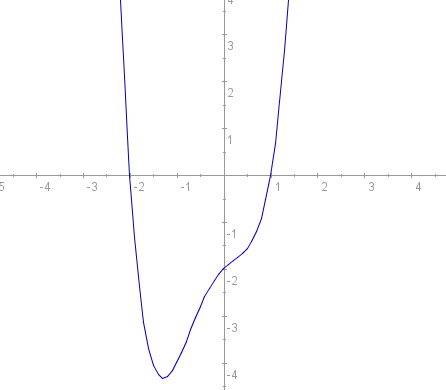
[Citat] %2.Sa se determine valorile parametrilor reali a si b pentru care multimea solutiilor inecuatiei x^4+x^3-x^2+ax+b=<0 este intervalul [-2,1].

Din enunt rezulta ca functia

ISI SCHIMBA SEMNUL IN x=-2 si x=1. Cu alte cuvinte, f(-2)=f(1)=0. Aceste fapte conduc la sistemul

cu solutiile a=1, b=2. Nu am terminat! Mai trebuie verificat faptul ca, intr-adevar, functia de mai sus ia valori negative exact pe intervalul [-2,1]. Acest lucru se verifica usor (studiul variatiei ...).

Fie cubul ABCDA1B1C1D1 cu muchia 1 si punctele M si N respectiv de pe segmentele AC si BD1, astfel incit masura ungiului NMC este de 60grade, masura unghiului MNB este de 45 de grade. Sa se determine lungimea segmentului MO, unde punctul O este centrul patratului ABCD.

Mc anticipat. Ionela

[Citat] Fie cubul ABCDA1B1C1D1 cu muchia 1 si punctele M si N respectiv de pe segmentele AC si BD1, astfel incit masura ungiului NMC este de 60grade, masura unghiului MNB este de 45 de grade. Sa se determine lungimea segmentului MO, unde punctul O este centrul patratului ABCD. Mc anticipat. Ionela

Figura

Rationam in felul urmator.

• Notam
  
  
  
• In triunghiul dreptunghic NMO un unghi are 60 de grade, deci
  
  
  
• Fie P proiectia lui M pe dreapta BD'. In treacat fie spus, acest punct nu depinde de M (teorema celor trei perpendiculare, etc.).
  
• Folosind asemanarea triunghiurilor BPO si BDD' calculam
  
  
  
• Aplicam teorema lui Pitagora in triunghiul POM. Obtinem
  
  
  
• In fine, deoarece triunghiul MPN este dreptunghic isoscel, avem
  
  

  
  
  

Parca am vazut ceva asemanator (dar pe dos) la testarea nationala de anul asta.

Problema
Sa se demonstreze ca daca lungimile laturilor unui triunghi dreptunghic formeaza o progresie aritmetica, atunci ratia acestei progresii este egala cu lungimea razei cercului inscris in triunghi.

Va multamesc.