| Autor |
Mesaj |
|
|
Salut,am cateva probleme si as vrea sa aflu cam cum se poat rezolva...
Calculati limitele sirurilor:
1) +...+(1+2+...+n)%5D%7D%7B1+2(1+2)+...+n(1+2+...+n)%7D)
2) 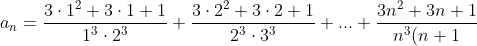%5E%7B3%7D%7D)
3) +...+a_%7Bk%7D&space;%5Cln&space;(n+k))&space;,a_%7B0%7D,a_%7B1%7D,...,a_%7Bk%7D%5Cin&space;R)
...ma chinui de ceva vreme sa gasesc o rezolvare, dar din pacate fara succes pana in momentul de fata. as fi tare bucuros daca primesc niste indicii pentru a rezolva sau chiar rezolvarea completa a acestor exercitii
---
Matematica este logica, functionala pur si simplu… minunata.
|
|
|
---
Doamne ajuta...
Petre
|
|
|
---
Doamne ajuta...
Petre
|
|
|
Mulţumesc!
La 3 m-am gandit sa dau factor comun fortat  ... dupa sa egalez limita cu  crezi ca pot scoate un raspuns "rezonabil" dupa calcul
---
Matematica este logica, functionala pur si simplu… minunata.
|
|
|
3)
Daca ai, cu i de la 1 la k este 0, e clar.
Altfel, limita tinde destul de repede spre +infinit, fiecare termen tinzand acolo, cand fiecare ai este >0.
Pentru fiecare ai <0 => limita este -infinit.
Partea urata este ca acei coeficienti pot alterna...
1) Numitorul este suma de la 1 la n din
[ (k^2)*(k+1)/2].
---
Pasionat de matematica
|
|
|
[Citat]
Mulţumesc!
La 3 m-am gandit sa dau factor comun fortat[ img]https://latex.codecogs.com/gif.latex?\ln&space;n[/ img] ... dupa sa egalez limita cu [img ]https://latex.codecogs.com/gif.latex?a_{0}+a_{1}+...+a_{k}[/ img] crezi ca pot scoate un raspuns "rezonabil" dupa calcul |
Va rog sa nu mai folositi imagini care se duc undeva altundeva.
Idea este de a refolosi codul, nu de a "face ceva ca sa se vadaceva".
Problema nu clarifica cine sunt termenii sirului
a0, a1, a2, ...
care intervin la acest punct (3).
Va rog sa precizati.
---
df (gauss)
|
|
|
[Citat]
[Citat]
Mulţumesc!
La 3 m-am gandit sa dau factor comun fortat[ img]https://latex.codecogs.com/gif.latex?\ln&space;n[/ img] ... dupa sa egalez limita cu [img ]https://latex.codecogs.com/gif.latex?a_{0}+a_{1}+...+a_{k}[/ img] crezi ca pot scoate un raspuns "rezonabil" dupa calcul |
Va rog sa nu mai folositi imagini care se duc undeva altundeva.
Idea este de a refolosi codul, nu de a "face ceva ca sa se vadaceva".
Problema nu clarifica cine sunt termenii sirului
a0, a1, a2, ...
care intervin la acest punct (3).
Va rog sa precizati. |
Salut ... nu prea am inteles partea cu atributul img Dar am sa ma straduiesc sa nu mai pun link-uri catre formule am sa pun codul direct
Problema nu specifica cine sunt termenii sirului ne spune doar ca ei apartin lui R
---
Matematica este logica, functionala pur si simplu… minunata.
|
|
|
De curand am dat peste urmatoarea problema...
Calculati limita sirului
a_{n} =\frac{1+a+...+a^{n-1}}{1+b+...+b^{n+1}} , a,b\in(0;1)
---
Matematica este logica, functionala pur si simplu… minunata.
|
|
|
[Citat]
De curand am dat peste urmatoarea problema...
Calculati limita sirului
a_{n} =\frac{1+a+...+a^{n-1}}{1+b+...+b^{n+1}} , a,b\in(0;1) |
Puteti tipari si afisa cele de mai sus pe pagina de fata in modul urmator.
Pentru tot textul sau doar pentru o parte folositi blocul pro-di numit equation.
In partea de editare este si un buton [LATEX] care - odata apasat - insereaza in locul cursorului acest bloc.
Eu o sa mai inserez un blank (loc liber) in acest bloc, deci
[eq uation]
[/eq uation]
cu blank dupa "eq", altfel mi se compileaza.
Atunci:
[eq uation]
Calculati limita sirului:
$$
a_{n} =\frac{1+a+\dots+a^{n-1}}{1+b+\dots+b^{n+1}}\ , \ a,b\in(0;1)\ .
$$
[/eq uation]
se compileaza in modul urmator:
Si solutia vine foarte repede, codul se refoloseste usor:
---
df (gauss)
|
|
|
Calculati limitele sirurilor:
---
Matematica este logica, functionala pur si simplu… minunata.
|
|
|
1.
Am ajuns pana la rezolvarea:
Prima limita stiu ca este egala cu 1 nu sunt sigur nu sunt sigur de a doua daca va rog daca ma puteti ajuta sa inteleg...
Albert Einstein:"Două lucruri sunt infinite: universul şi prostia omenească, şi încă nu sunt sigur de primul." eu nu sunt sigur de amandoua =))
---
Matematica este logica, functionala pur si simplu… minunata.
|


