Buna seara
Fie ABC un triunghi ascutitunghic cu ortocentrul H si A',B',C'picioarele inaltimilor duse din A ,B si respectiv C.
Notam cu S intersectia dreptei AC cu dreapta C'M,unde M este mijlocul lui [BC].
Paralela prin S la BC intersecteaza dreapta AB in Q.Aratati ca punctele Q,A',B'
sunt colineare.
multumesc

[Citat] Buna seara Fie ABC un triunghi ascutitunghic cu ortocentrul H si A',B',C'picioarele inaltimilor duse din A ,B si respectiv C. Notam cu S intersectia dreptei AC cu dreapta C'M,unde M este mijlocul lui [BC]. Paralela prin S la BC intersecteaza dreapta AB in Q.Aratati ca punctele Q,A',B' sunt colineare. multumesc

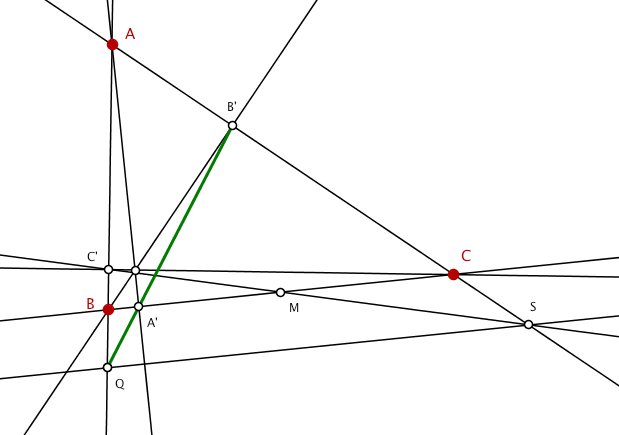
In triunghiul ABC se pot face urmatoarele:

• Se scrie teorema lui Ceva pentru ortocentru.
  
• Se scrie teorema lui Menelaus pentru dreapta C'S.
  
• Se aplica reciproca teoremei lui Menelaus pentru punctele Q, A', B'.
  

Solutie alternativa:

(Aceleasi notatii ca in figura de mai sus, candva voi invata si eu sa desenez si sa postez...)

B'C'BC este inscriptibil, unghiul exterior din C' este deci de aceeasi masura cu cel interior din C.
Avem paralelitatea BC || QS.
Deci si B'C'QS este inscriptibil.

(Altfel scris B'C' este o antiparalela pentru BC, deci si pentru QS.)

Unghiul <(B'C'S) este de masura lui <(A) . Deoarece este
180° - <(BC'M) - <(AC'B')
= 180° - <(B) - <(C)
= <(A) .
(Dar de fapt nici nu ne trebuie acest calcul...)

Deci si <(B'QS) este din inscriptibilitate tot <(A) .

In patrulaterul inscriptibil B'C'A'M (Euler, mai sunt alte cinci puncte pe cercul lui...) avem de asemenea <(B'A'M) = <(B'CM) = <(A) .

Deci B'A' si B'Q sunt doua drepte prin B' care fac cu paralelele BC si QS acelasi unghi. Rezulta coliniaritatea.

[Citat] Solutie alternativa: ... ...

Aha, aveam o banuiala ca se poate si fara asemanare. Vreau numai sa mentionez ca prima solutie ramane valabila daca schimbam ortocentrul cu un punct oarecare.