| Autor |
Mesaj |
|
|
Pentru ce valori reale ale lui a si b, ecuatia:
are o singura radacina reala?
|
|
|
[Citat]
Pentru ce valori reale ale lui a si b, ecuatia:
are o singura radacina reala? |
E clar ca, odata gasit b, coeficientul a este arbitrar. De asemenea, e clar ca b=0 este unul dintre raspunsuri. Vom cauta mai jos valorile nenule ale lui b.
In alta ordine de idei, deoarece
, acel membru stang are un minim. Prin urmare, daca a,b satisfac cerintele problemei atunci musai acel minim trebuie sa fie egal cu
(!!!).
Notam
. Trebuie gasita valoarea minima a functiei
conditionat de
. Cu multiplicatorii lui Lagrange formam functia
Punctul de minim conditionat, daca exista (si el exista!), este punct critic al acestei functii, adica
De aici rezulta
. Deoarece f ia valoarea
in acest punct folosim argumentul (!!!) de mai sus si gasim
Cazul b=0 a fost transat, iar cazul b=1 este si el valid. Nu am facut toate calculele dar graficul functiei
arata astfel: 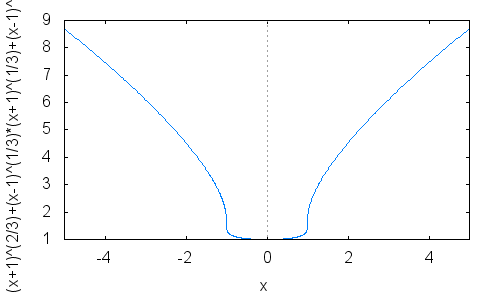
---
Euclid
|
|
|
Multumesc! Frumoasa rezolvare! In fine, problme se termina "tragic"(acum ma gandesc numai la Baltagul  ) ) cu impunerea conditiei
din conditia unicitatii solutiei.
|
|
|
|
|
|
Corectissim!
P.S. Functia este impara.
---
Euclid
|
|
|
[Citat]
P.S. Functia este impara. |
Sigur?
|
|
|
[Citat]
[Citat]
P.S. Functia este impara. |
Sigur? |
Aveti dreptate, este functia este para.
---
Euclid
|
|
|
[Citat]
In alta ordine de idei, deoarece
, acel membru stang are un minim. Prin urmare, daca a,b satisfac cerintele problemei atunci musai acel minim trebuie sa fie egal cu
(!!!).
|
Imi puteti explica, va rog, de ce trebuie ca
sa fie minimul? (m-am mai gandit la problema si nu stiu ce sa zic, x practic are o singura valoare (sper sa ma insel...ca imi place rez dvs :D ))
Va multumesc!
|
|
|
[Citat]
Imi puteti explica, va rog, de ce trebuie ca
sa fie minimul? |
In primul rand exista un minim global
m = f(xmin)
al functiei *continue* in discutie.
(Infimumul exista, la el tinde un sir de valori pentru un sir de abscise, ultimul trebuie sa fie marginit, luam un subsir convergent...)
Daca m > c nu avem nici o solutie a ecuatiei...
Daca m = c avem ce vrem.
Daca m < c, din teorema lui Darboux exista cel putin o valoare pe
( -oo, xmin ) respectiv pe
( xmin , +oo )
unde se ia valoarea intermediara c. Dar noi vrem solutie unica...
---
df (gauss)
|
|
|
Nu va suparati pe mine, dar sunt mai batut in cap :D si nu prea am inteles. (vreau sa inteleg "metoda" ca sa o mai pot aplica si alta data  )
1. De ce in cazul m>c nu avem solutii?
2. Despre care teorema a lui Darboux vorbiti?
Va multumesc!
|
|
|
[Citat]
Nu va suparati pe mine, dar sunt mai batut in cap :D si nu prea am inteles. (vreau sa inteleg "metoda" ca sa o mai pot aplica si alta data  ) )
1. De ce in cazul m>c nu avem solutii?
2. Despre care teorema a lui Darboux vorbiti?
Va multumesc! |
Trebuie sa ma leg explicit de obiecte.
Sper ca lucrurile devin mai clare.
Fixarea structurala a cunostintelor de asa natura incat drumul normal prin matematica sa permita pasi naturali este un lucru important. Manualele nu sunt scrise neaparat cu acest gand in fundal.
Dupa liceu mi-am ajustat de mai multe ori modul de percepere a celor invatate in liceu... Nu a fost mereu usor, de aceea incerc sa vin la timp un un fel de anticipare a flexibilitatii.
---
df (gauss)
|


