| Autor |
Mesaj |
|
|
Un tablou este atârnat într-un cui pe perete. E clar c? dac? scoatem cuiul din perete, tabloul cade!
Întrebare. Este posibil s? atârn?m tabloul în trei cuie, astfel încât, dac? scoatem oricare cui din cele trei, tabloul s? cad? ??????????
---
Euclid
|
|
|
Da, e posibil, pentru orice
cuie.
Pentru a se în?elege mai bine cerin?a problemei, iat? o solu?ie posibil? pentru 2 cuie: 
Uploaded with ImageShack.us
|
|
|
S? not?m cuiele cu A,B,C. S? not?m cu
ac?iunea "înf??ur?m sfoara o dat? în jurul cuiului A in sens orar" ?i cu
ac?iunea "înf??ur?m sfoara o dat? în jurul cuiului A in sens antiorar". La fel pentru B ?i C. Astfel, desenul din postarea de mai sus corespunde expresiei
(desigur, juxtapunerea semnific? efectuarea succesiva a ac?iunilor.) De exemplu,
înseamn? c? înf?suram o dat? sfoara in jurul lui A în sens orar, apoi o dat? în sens antiorar. Evident, tabloul cade în acest caz.
Solu?ia problemei noastre:
|
|
|
Exact! Henri Poincaré a introdus acum mai bine o sut? de ani grupul fundamental.
Avem de-a face cu un spa?iu care "seam?n?" cu un plan din care am scos trei puncte (cuiele). Întrebarea este dac? o curb? în acest spa?iu (sfoara) poate fi deformat? într-un punct f?r? a o trece în mod for?at peste "g?uri" ( ac?iunea de deformare se nume?te omotopie ).
Ei bine, curbele închise ce trec printr-un punct fix, împreun? cu omotopia ca rela?ie de echivalen??, formeaz? un grup. Opera?ia de grup este concatenarea curbelor... Mai mult, grupul ob?inut nu depinde de punctul fix ales.
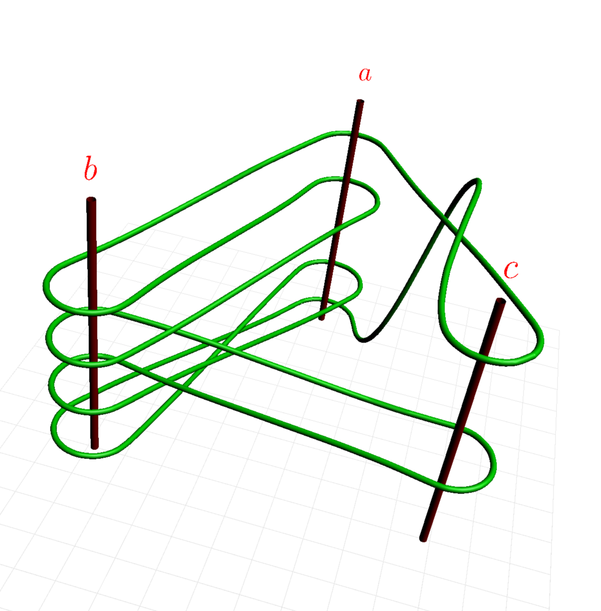
Grupul nostru este grupul liber cu trei generatori ( a, b, c ).
Iat? elementul
: 
Pentru n=2 grupul fundamental este grupul liber cu doi generatori, iar elementul
arat? astfel: 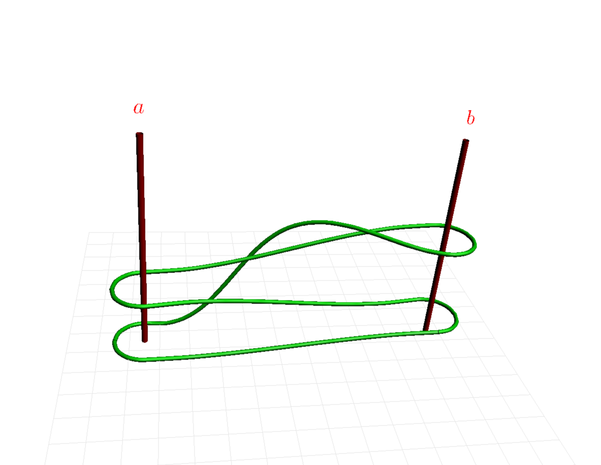
---
Euclid
|
|
|
(Pentru cei ce stiu ce e un nod...)
Probabil ca trebuie la modelare sa fim mai atenti. Problema este mai degraba una de forma:
Fie d1, d2, ... , dn drepte paralele in spatiul euclidian 3-dimensional real.
Introducem notatiile:
Avem desigur scufundari ale lui X in spatiile celelalte ce au cate o dreapta (un obstacol) mai putin. Problema cere (probabil) sa aratam ca exista un nod K in X care este netrivial, astfel incat mutat covariant prin fiecare din scufundarile
sa devina trivial...
Deoarece eu am inca necazuri cu nodurile in
, nu vreau sa mai insist. (Probabil ca ma insel la modelare, dar am zis sa zic mai bine...)
---
df (gauss)
|
|
|
[Citat]
(Pentru cei ce stiu ce e un nod...)
Probabil ca trebuie la modelare sa fim mai atenti. Problema este mai degraba una de forma:
... ...
Deoarece eu am inca necazuri cu nodurile in
, nu vreau sa mai insist. (Probabil ca ma insel la modelare, dar am zis sa zic mai bine...) |
Sunt de acord c? sunt capcane. De exemplu, chiar dac? curba este nul omotop?, este posibil s? nu se desf??oare f?r? "s? treac? prin ea îns??i". Totu?i, solu?ia de mai sus func?ioneaz?.
---
Euclid
|


