În plan se consider? n?3 puncte cu proprietatea c? pentru oricare trei exist? un disc de raz? unu care le acoper?.S? se demonstreze c? exist? un disc de raz? unu care acoper? toate cele n puncte.

E teorema Helly: fiind date n multimi convexe in plan astfel ca intersectia oricaror 3 sa fie nevida, atunci intersectia tuturor e nevida.

E suficient sa consideram discurile de raza 1 centrate in punctele respective.

[Citat] E suficient sa consideram discurile de raza 1 centrate in punctele respective.

...care vor avea asadar intersectia nevida.Si apoi cum gasesc discul care la acopera pe toate?

[Citat] [Citat] E suficient sa consideram discurile de raza 1 centrate in punctele respective. ...care vor avea asadar intersectia nevida.Si apoi cum gasesc discul care la acopera pe toate?

E teorema Helly: fiind date n multimi convexe in plan astfel ca intersectia oricaror 3 sa fie nevida, atunci intersectia tuturor e nevida.

[Citat] [Citat] [Citat] E suficient sa consideram discurile de raza 1 centrate in punctele respective. ...care vor avea asadar intersectia nevida.Si apoi cum gasesc discul care la acopera pe toate? E teorema Helly: fiind date n multimi convexe in plan astfel ca intersectia oricaror 3 sa fie nevida, atunci intersectia tuturor e nevida.

Discurile centrate in punctele respective sunt multimile convexe?

[Citat] Discurile centrate in punctele respective sunt multimile convexe?

Da.

[Citat] În plan se consider? n?3 puncte cu proprietatea c? pentru oricare trei exist? un disc de raz? unu care le acoper?.S? se demonstreze c? exist? un disc de raz? unu care acoper? toate cele n puncte.

Încerc s? schi?ez o solu?ie specific? (pentru discuri). Trec peste am?nunte legate de compacitate (care sunt ascunse ?i în teorema lui Helly, Hahn-Banach, etc.).

Not?m cu P proprietatea unor discuri ca în enun? (de raze egale dar nu neap?rat cu unitatea). Fie

centrele discurilor. Fie M mul?imea numerelor reale r cu proprietatea c? discurile de raze r centrate în

satisfac proprietatea P. Atunci M este un interval de forma

. Ne uit?m acum la cercurile centrate în punctele date, de raze R.

Avem dou? cazuri. În primul caz, exist? trei cercuri ce se intersecteaz? într-un punct ca în figura urm?toare.



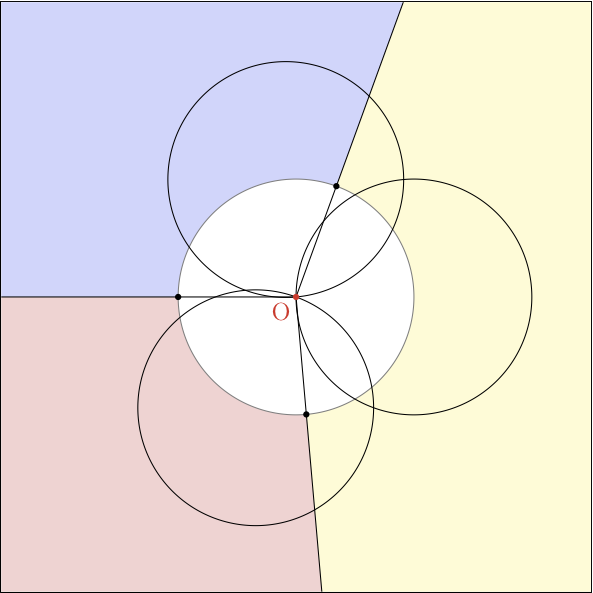
Regiunile mioritice din figur? sunt determinate de simetricele centrelor celor trei cercuri fa?? de punctul de intersec?ie comun. Se arat? c? toate celelalte puncte apar?in neap?rat discului alb (din minimalitatea lui R)

Al doilea caz este mai simplu, anume exist? dou? cercuri tangente.



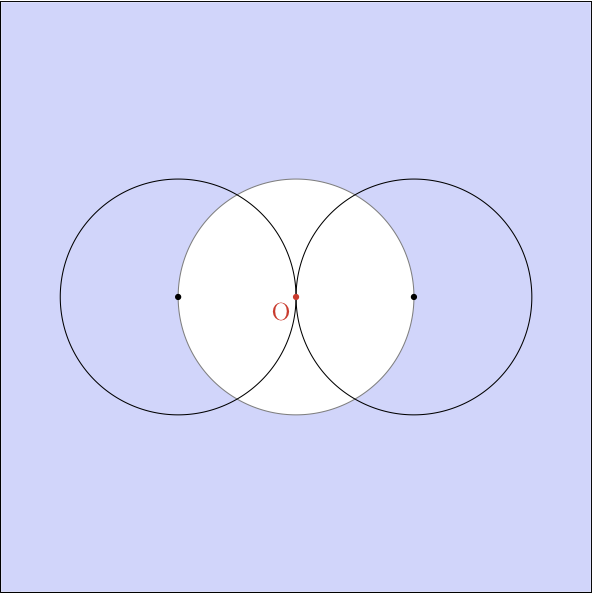
Din nou, e clar c? toate punctele apar?in discului alb.