Vom presupune c? plantele sunt situate în puncte cu coordonate numere întregi.
Fie (a,b) coordonatele unei plante oarecare. Atunci planta este vizibil? (cel pu?in par?ial) din origine dac? ?i numai dac?
- Numerele a, b sunt prime între ele.
- Punctul (a,b) este situat în interiorul discului centrat în origine de raz? 1/r.
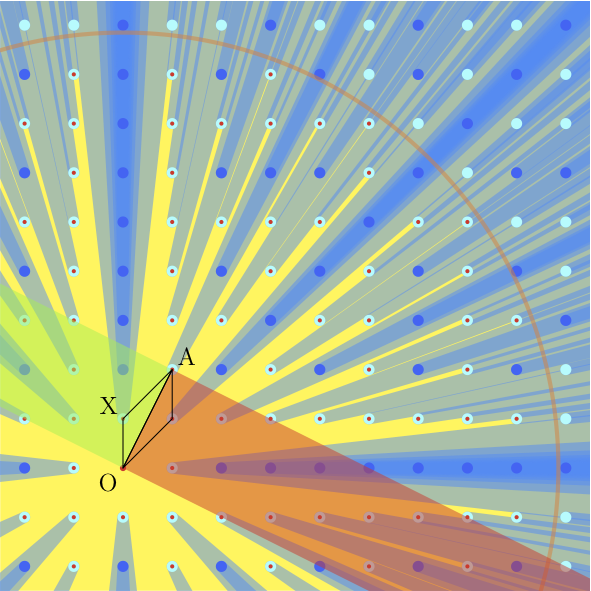
Fie
A(a,b) un punct cu coordonatele întregi. "Banda" care are segmentul
OA ca l??ime se împarte în dou? regiuni, ca în figur?. Punctul
A este invizibil din origine dac? ?i numai dac? exist? un punct cu coordonate întregi în acea band?, situat fa?? de segmentul
OA la distan?? cel mult egal? cu
1/r. Din motive de simetrie (vezi paralelogramul din figur?), acest punct ipotetic poate fi presupus ca apar?inând jum?t??ii verzi ai benzii noastre !
Fie
X punctul cu coordonate întregi din regiunea verde aflat la distan?a minim?
d fa?? de segmentul
OA (acel punct exist?!!!!). Evident, dac? numerele întregi
a, b au un divizor comun netrivial, punctul
A nu este vizibil din origine. În caz contrar, din motive de minimalitate, triunghiul
OAX nu con?ine puncte cu coordonate întregi, altele decât cele trei vârfuri. Conform teoremei lui
Pick, aria sa este egal? cu
1/2. Cu alte cuvinte
. Condi?ia
revine la


