Sa se determine b si c numere reale strict pozitive, astfel incat: c^x+b^x>=x^c+x^b, oricare ar fi x >0.
O solutie am observat-o: b=c=e...dar nu pot demonstra ca e unica. Are cineva vreo sugestie?

Ca element ajutator, iata o propozitie in drumul spre solutie:

Pentru orice

are loc inegalitatea

cu egalitate daca si numai daca

.

Argument:
Logaritmam ambele parti in inegalitatea ce este de demonstrat, obtinand o inegalitate echivalenta (cu egalitate in acelasi caz, deoarece logaritmul este functie strict crescatoare).
Consideram atunci functia ajutatoare

.

Derivata a doua este strict pozitiva (h este strict convexa),

deci h' este strict crescatoare, iar din h'(e)=0 rezulta ca h' este strict negativa pe (0,e), egala cu zero in e si strict pozitiva pe (e,infinit). (Acest lucru se face desigur "banal" sau "ochiometric", si fara apel la derivata a doua, dar convexitatea da suport intuitiv la ceea ce urmeaza...)

deci -stiind semnul lui h'- rezulta ca h este strict descrescatoare pe (0,e] si strict crescatoare pe [e, infinit). Punctul e este minim absolut al functiei date.

Cum se rezolva acum problema de mai sus?

Ok, demonstratia acelei propozitii am facut-o si eu, tot prin logaritmare si apoi aplicand sirul lui Rolle. Asa am ajuns la concluzia ca e este o solutie, si da, fiind punct de minim local si al functie mele, din Teorema lui Fermat rezulta ca derivata in e este 0. Numai ca ecuatia la care ajung...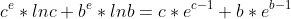

nu stiu sa o rezolv...

Bun, consideram functia

Ce se poate spune despre g(e) ?

P.S. Am apreciat mult gasirea cazului particular b=c=e... Din respect am venit numai pana la jumatate de drum...

g(e)<=0, cu egalitate pt b=c=e.
dar eu am nevoie ca g(e)>=0, deci practic g(e) trebuie sa fie egal cu 0, deci b=c=e. Gresesc? Multumesc mult pentru timpul acordat.

Noua ni se da

pentru orice x>0, deci in particular si pentru x=e. Dar cu observatia tocmai facuta avem

cu exceptia cazului in care b=c=e.

Deci numai cazul b=c=e intra in discutie pentru o solutie, iar cu cele ce mai sus, dam intr-adevar de o soultie...