1. Fetele laterale ale unei piramide triunghiulare regulate cu interiorul gol, sunt oglinzi perfecte. Prin centrul bazei patrunde in interior o raza de lumina. Un foton al ei, se da cu capul de pereti de 6 ori, apoi iese (probabil ametit) pe unde a venit.
a) Ce relatie trebuie sa fie intre a-latura bazei si h-inaltimea piramidei, pentru ca afirmatia din enunt sa poata fi adevarata?
b) Care este numarul de solutii in cazul a) si cate sunt distincte?(ca lungime a drumului parcurs de foton)
c) Pentru

, sa se calculeze distanta maxima pe care o poate parcurge fotonul in interiorul piramidei, cand indeplineste conditia din enunt, si distanta minima.

2. Acelasi enunt pentru piramida patrulatera.

O mica indicatie se afla sub acest buton

Problema se rezolv? considerând simetrii succesive fa?? de fe?ele laterale. Cel mai simplu de rezolvat ar fi cu calculatorul. Dac? ave?i r?bdare povesti?i-ne m?car în linii mari metoda dvs.

[Citat] Problema se rezolv? considerând simetrii succesive fa?? de fe?ele laterale. Cel mai simplu de rezolvat ar fi cu calculatorul. Dac? ave?i r?bdare povesti?i-ne m?car în linii mari metoda dvs.

As fi curios sa vad cum se poate rezolva cu ajutorul calculatorului(eu nu prea ma pricep sa-l folosesc!).
Cum am rezolvat eu, se poate vedea aici:
http://proftelteu.wikispaces.com/prima+pagina

M-am uitat pe link-ul de pe wikispaces, hm, respect pentru munca depusa.
(Latex+pdf ar fi usurat poate efortul, dar sunt subiectiv la aceasta afirmatie.)

Ma refer numai la cazul unei piramide patrulatere.
La inceput si eu am fost inclinat sa folosesc calculatorul, algoritmul fiind cam urmatorul:

Se fixeaza V(0,0,0)

Se dau a,h simbolice si se construieste piramida (P0)=VABCD de inaltime h si de latura a. Ne intereseaza poate mai mult R=VA.

Fie (S) sfera de centru V ce trece prin A,B,C,D. Ea are raza R.

Plecand cu piramida P1 se construiesc siruri de piramide in reflexie fata de fetze. Obtinem mai multe lanturi ( P0, P1, P2, ... , PN ).

Cel mai bine desenam toate lanturile prin proiectii din V ale bazelor piramidelor P0, P1, P2, ..., P6 pe un plan paralel cu (ABCD). Calculatorul le poate plota si calcula simbolic.
Cred ca un desen proiectie stereografica pentru "drumul drept" ar ajuta mult la formarea intuitiei in 3D.

Fie X0, ..., XN centrele piramidelor construite. Dreapta (X0,XN) este atunci o solutie, daca ea nu "iese din peisaj", adica daca taie intotdeauna fatza fatza de care s-a luat reflexia la trecerea de la o piramida la alta.

Deoarece problema are atat o parte combinatorica, cat si una de "programare liniara" este greu de "vandut" publicului. Dupa parerea mea, AMM ar fi o revista interesata de publicat problema cu solutia, daca prezentarea este compacta si cu imagini sugestive. (AMM vaneaza tot ce este intuitiv!) O sa incerc sa scriu cateva randuri de cod... dar nu pot promite nimic acum.

F?r? calculator problema ar fi mai potrivit? într-o rubric? denumit? "problema trimestrului".

În orice caz, gauss a descris exact metodologia potrivit?.

FIX?M UNE DINTRE FE?E ?I PESUPUNEM C? ESTE PRIMA FA?? LOVIT? DE FOTON.
Folosind maxima, începem prin a defini reflec?ia fa?? de planul determinat de doi vectori:

[Cod] sim(A,B,x):=block( [L,a,b], L:solve( [a*dotproduct(A,A)+b*dotproduct(A,B)-dotproduct(A,x),a*dotproduct(B,A)+b*dotproduct(B,B)-dotproduct(B,x)],[a,b]), return( ev( 2*(a*A+b*B)-x, first(L),trigsimp,radcan,ratsimp ) ) );

Func?ia urm?toare genereaz? numerele a,b,1-a-b, unde primele dou? numere sunt coeficien?ii vectorului de intersec?ie al planului generat de doi vectori A, B cu dreapta determinat? de doi vectori x,y (fa?? de baza (A,B))

[Cod] test_hit(AA,BB,x,y):=block( [LL], LL:solve( part(transpose(x+t*(y-x)-a*AA-b*BB),1),[t,a,b] ), return( ev( [a,b,1-a-b], first(LL),ratsimp,trigsimp ) ) );

Cele trei numere trebuie s? fie pozitive dac? dorim s? în?ep?m triunghiul cu laturile A,B.

Not?m cu h, r în?l?imea, respectiv raza bazei piramidei. Not?m

.

Func?ia urm?toare calculeaz? toate listele posibile de reflec?ii succesive.

[Cod] photon3(num_reflections):=block( [L,U,SL,A,B,C,x,n], A:transpose(matrix([r,0,h])), B:transpose(matrix([-r/2,sqrt(3)*r/2,h])), C:transpose(matrix([-r/2,-sqrt(3)*r/2,h])), x:transpose(matrix([0,0,h])), L[0]:[ C, A, B, x ], U:[ sim(A,B,C),A,B,sim(A,B,x) ], print("U=",U), L[1]:[append(L[0],U)], for i:2 thru num_reflections do ( print("i=",i), L[ i]:[], for SL in L[i-1] do ( n:length(SL), C:SL[n-3], A:SL[n-2], B:SL[n-1], x:SL[n], L[ i]:append(L[ i],[append(SL,[sim(C,A,B),C,A,sim(C,A,x)])]), L[ i]:append(L[ i],[append(SL,[sim(C,B,A),C,B,sim(C,B,x)])]) ) ), return(L[num_reflections]) ); results3:''photon3(6)$

Func?ia urm?toare se ocup? de oricare din listele (32 la num?r) tocmai ob?inute:

[Cod] test_case(LL):=block( [n,i,R], R:[], n:length(LL)/4, for i:2 thru n do ( R:append(R,ev(test_hit(LL[4*(i-1)+2],LL[4*(i-1)+3],LL[4],LL[4*n]),ratsimp,factor)) ), return(R) );

Lungimea traseului (ipotetic) pentru fiecare din liste este:

[Cod] p_distance(LL):= ev( mat_norm(LL[4]-last(LL),frobenius), ratsimp, factor,radcan,factor );

Analiza final?:

[Cod] final_analysis(LL):=block( [SL,i,SLP,lstr,U,V], i:1, for SL in LL do ( print("case ",i), i:i+1, lstr:"CAZ INVALID:", SLP:test_case(SL), U:limit(SLP,u,0), V:limit(diff(SLP,u),u,0), print(U), print(V), if apply(min,U)>0 then lstr:"CAZ VALID:" else ( if apply(min,U)>=0 then ( if apply(max,(U+V+abs(U-V)/2))>0 then lstr:"VALID CASE:" ) ), print(lstr,p_distance(SL)) ) );

Ob?inem 6 cazuri posibil valide, care din punctul de vedere al lungimii traseului fotonului, se reduc la numai dou? cazuri. Mai precis:

• Pentru u<0,2264135448674914 (cea mai mic? r?d?cin? pozitiv? a polinomului
  
  ) lungimile posibile ale traseului sunt, în ordinea invers? a m?rimii:
  
  
  
  
• Pentru 0,2264135448674914<u<0,3559102994032652 (cea mai mic? r?d?cin? pozitiv? a polinomului
  
  ) prima variant? din cazul de mai sus nu mai e posibil?, doar a doua.
  

Exemplu de traseu lung (desf??urat conform planului):

Exemplu de traseu mai scurt (a doua variant? posibil?):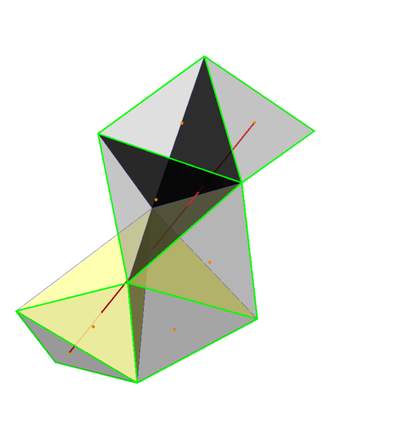


Am l?sat sub t?cere o mul?ime de am?nunte. Calculele pot fi verificate... În orice caz, morala este c?... este posibil.

Se pare ca ar trebui sa ma apuc de studiat MAXIMA, dar din ce am vazut-gasit despre ea, ma sperie mai ceva ca LaTeX-ul prima data, si nici nu sunt convins ca merita efortul.