buna dimineata,
n-am facut vectori la scoala si am probleme mari cu ei.
Varianta...004
SUBIECTUL I
a) zice ca am punctele A(3;3) si B(-1;1) si sa determin coordonatele lui AB si la b) sa determin lungimea vectorului AC
Varianta...007
SUBIECTUL I
e) zice sa calculez produsul scalar al v1(1,radical din 2) si v2(radical din 2,-1).
seamana si nu prea cu Varianta...024 a) v = 3i + 2j si w = 2i - 3j si se cere produsul scalar. Nu stiu cum vine.
Varianta...002
SUBIECTUL I
c) zice sa se arate ca vectorul 4i + 3j are lungimea egala cu 5. e ceva cu pitagora aici parca.
Varianta...008
se considera vectorii OA = -i â?? 5j, OB = 5i + 3j si OC = 5i â?? 5j
Si imi cere a) lungimea segementului [AB] si d) lungimea vectorului AC
Adica daca am un vector scris in functie de i si j cum calculez lungimea, si daca nu e scris functie de i si j cum o calculez oricum ca la ...004 I, a), coordonatele unui vector si tot asa. si inca ceva, produsul vectorial a 2 vectori nu-i tot una cu cel scalar. n-am gasit asa ceva deocamdata in nici o varianta dar cum se face. e ceva cu sin de nu stiu ce.

[Citat] buna dimineata, n-am facut vectori la scoala si am probleme mari cu ei.

Daca e clar cum ne putem orienta in plan avand un sistem de axe, ce ne facem daca nu-l avem? La urma urmei, e o conventie ca oricare alta. Ei bine, inventam vectorii. Intuitiv, ei contin doua "marimi":

• o directie (e.g. nord-nord-vest)
  
• o lungime
  

Cel mai simplu exemplu este viteza: directia in care ne deplasam si viteza propriu-zisa (cat de repede). De aceea vectorii se reprezinta cu sageti (o sageata are o directie si o lungime).
In figura de mai jos toate sagetile au aceeasi directie si lungime deci reprezinta unul si acelasi vector. Din aceasta cauza, pentru ca sa reprezentam deplasarea dintr-un punct in altul, reprezentam algebric vectorii prin diferenta coordonatelor celor doua puncte.

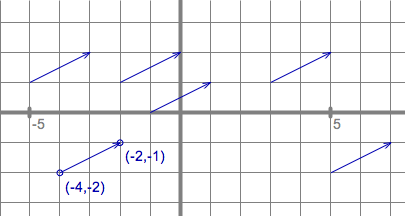
De exemplu vectorul din figura este

. Aici am presupus ca avem totusi un sistem de axe. Fixand insa vectorii

putem sterge axele, pentru ca acum reprezentam orice vector din plan ca o combinatie ai celor doi (de aceea perechea i,j se numeste baza). revenind la vectorul nostru, scriem

Adunarea vectorilor se face pe coordonate. Lungimea vectorului se calculeaza cu teorema lui Pitagora. Ma opresc aici.

[Citat] Varianta...004 SUBIECTUL I a) zice ca am punctele A(3;3) si B(-1;1) si sa determin coordonatele lui AB si la b) sa determin lungimea vectorului AC

ca mai sus, avem

deci

(am calculat lungimea lui ab, ca nu stiu cine e C

[Citat] Varianta...007 SUBIECTUL I e) zice sa calculez produsul scalar al v1(1,radical din 2) si v2(radical din 2,-1). seamana si nu prea cu Varianta...024 a) v = 3i + 2j si w = 2i - 3j si se cere produsul scalar. Nu stiu cum vine.

Sunt multe de spus. Produsul scalar este un numar si se obtine inmultind vectorii pe coordonate si sumand. Deci

[Citat] Varianta...002 SUBIECTUL I c) zice sa se arate ca vectorul 4i + 3j are lungimea egala cu 5. e ceva cu pitagora aici parca. Varianta...008 se considera vectorii OA = -i â?? 5j, OB = 5i + 3j si OC = 5i â?? 5j Si imi cere a) lungimea segementului [AB] si d) lungimea vectorului AC Adica daca am un vector scris in functie de i si j cum calculez lungimea, si daca nu e scris functie de i si j cum o calculez oricum ca la ...004 I, a), coordonatele unui vector si tot asa. si inca ceva, produsul vectorial a 2 vectori nu-i tot una cu cel scalar. n-am gasit asa ceva deocamdata in nici o varianta dar cum se face. e ceva cu sin de nu stiu ce.

Produsul scalar are si o interpretare geometrica. Produsul vectorial e intr-adevar cu totul altceva, si nici macar nu exista in plan. Se face mai mult la fizica prin liceu (regula mainiidrepte nu suna cumva cunoscut?)

acum da, parca mai face sens...
C era (2;5) -- mi-a scapat.
in afara de vectori doar 1 mare amaraciune as mai avea (cred).
e despre punctele de extrem local, global, de inflexiune si cele critice si tot asa. e cu puncte... nu stiu care cu care si cand se intampla in legatura cu derivatele care si cand nu. dar trebuie sa imi mai iau niste timp sa vad cum sa intreb ca nu stiu de unde sa o apuc mai concret asa. dar imi dau seama ca stiti deja ce vreau sa intreb.

si regula mainii drepte suna chiar cunoscut. mie, cel mai tare imi placea la fizica. la noi, la fizica, profesorul zicea de-o musca care zboara si face cu gravitatia o treaba. si musca tot facea asa vreme de 1 an. si cand mi-am dat seama ca o sa dau bac-ul si la fizica, m-am apucat de citit regula mainii drepte. deci e logic.

[Citat] in afara de vectori doar 1 mare amaraciune as mai avea (cred). e despre punctele de extrem local, global, de inflexiune si cele critice si tot asa. e cu puncte... nu stiu care cu care si cand se intampla in legatura cu derivatele care si cand nu. dar trebuie sa imi mai iau niste timp sa vad cum sa intreb ca nu stiu de unde sa o apuc mai concret asa. dar imi dau seama ca stiti deja ce vreau sa intreb.

Credem ca v-ar fi util sa parcurgeti problemele noastre rezolvate (va puteti si testa cu ele) de la

http://www.pro-didactica.ro/probleme/browserez.php?t1=Analiza+matematica&t2=Functii+derivabile&cuv=Studiul+variatiei+unei+functii+cu+ajutorul+derivatelor

sau din meniul din stanga alegeti pe rand:

"Probleme

"Analiza matematica"

"Functii derivabile"

"Studiul variatiei unei functii cu ajutorul derivatelor"

urmat de butonul "Vezi problemele" din josul paginii.

nu luasem seama pana acum la Problemele de pe site.
a fost foarte foarte util si cred ca am inteles bine.
va multumesc.