Numim functi "olimpica" o functie f:RxR->R, cu proprietatea:
"Daca A1,A2,...,An sunt puncte distincte si f(A1)=F(A2)=...=f(An), atunci A1, A2,..,An sunt varfurile unui poligon convex".
Demonstrati ca daca P este un polinom neconstant, atunci functia f:RxR->R,
f(x,y)=|P(x+iy)| este olimpica <=> P are toate radacinile egale.

[Citat] Numim functi "olimpica" o functie f:RxR->R, cu proprietatea: "Daca A1,A2,...,An sunt puncte distincte si f(A1)=F(A2)=...=f(An), atunci A1, A2,..,An sunt varfurile unui poligon convex". Demonstrati ca daca P este un polinom neconstant, atunci functia f:RxR->R, f(x,y)=|P(x+iy)| este olimpica <=> P are toate radacinile egale.

Ne ocupam doar de implicatia netriviala. Presupunand prin absurd ca o functie olimpica are doua radacini distincte

, ajungem la situatia absurda din figura:

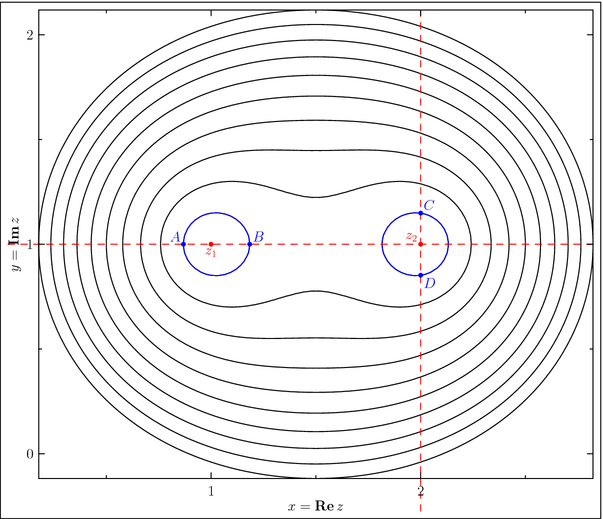
Curbele albastre corespund unei curbe de nivel

, unde c>0 este o constanta suficient de mica. Dreptele punctate cu rosu sunt perpendiculare si trec prin punctele de afix

. Punctele A,B,C,D sunt pe cele doua drepte de o parte si de alta a radacinilor, etc. Evident, cele patru puncte de mai sus nu sunt varfurile unui patrulater convex.

Nu intram in detalii pentru ca riscam sa nu vedem padurea din cauza copacilor.