| Autor |
Mesaj |
|
|
Fie a apartine R+ si z apartine C, a.i. |z+1/z|=a. Sa se determine cea mai mare si cea mai mica valoare posibila a lui |z|
|
|
|
Si eu sunt din tm si ti-as sugera sa scrii eventual ce exercitiu este si din ce sectiune ca poate o am rezolvata si e mai usor sa o am in fata cand o scriu pe comp...(fara sa o rezolv din nou) 
---
Viata e complexa, are atat parte reala cat si parte imaginara.
|
|
|
AL-231
|
|
|
Ok, o am Sper sa ajung sa postez rezolvarea in seara asta.
---
Viata e complexa, are atat parte reala cat si parte imaginara.
|
|
|
Scuze de intarziere, probleme cu internetul.
Se foloseste urmatoare propozitie:
||a|-|b||<=|a+b|<=|a|+|b|, oricare ar fi a,b nr complexe.
Se aplica pentru a=z si b=1/z.
---
Viata e complexa, are atat parte reala cat si parte imaginara.
|
|
|
[Citat]
Scuze de intarziere, probleme cu internetul.
Se foloseste urmatoare propozitie:
||a|-|b||<=|a+b|<=|a|+|b|, oricare ar fi a,b nr complexe.
Se aplica pentru a=z si b=1/z. |
Am aplicat pt a=z si b=1/z, dar tot nu imi dau seama cum se face mai departe...
Am ajuns la
|z^2-1|/a<=|z|<=(z^2+1)/a
|
|
|
Nu e un exercitiu usor. Se scrie z sub forma trigonometrica,
si atunci
Din conditia pusa se obtine o ecuatie bipatrata pentru
, cu parametrul
. In final, se alege
pentru ca
sa fie maxim/minim.
|
|
|
Pentru alta solutie, vezi problema 337 de aici http://ilib.mirror1.mccme.ru/djvu/bib-mat-kr/shk-1.djvu
( e in limba rusa ) pagina 351
|
|
|
In figura de mai jos sunt reprezentate curbele de nivel ale respectivei functii. Figura sugereaza faptul ca atat minimumul cat si maximumul trebuie cautate pe axele de coordonate.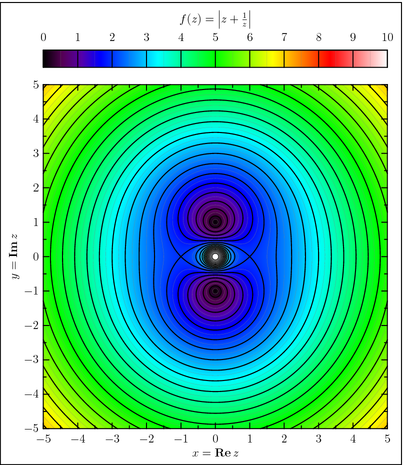 
---
Euclid
|
Access general
Conţine mesaje necitite
